|
|
|
|
|
|
Procedual Content Generation Tips
L-system
TODO
Wave Function Collapse

- Gridify the space. Populate it with the initial values.
- Iterate the empty cells and record the possible values that can be put in each. The number of the viable values for a grid is defined as its entropy.
- Iterate the grid with the minimum postive entropies and select one value to fill in.
- Keep looping until all entropy is non-postive.
Noise
Useful Fade Function
Rather than just using linear interpolation, we can use a fade function.
Useful Random Functions
- GLSL Noise Algorithms.
- float, small and random - 2005
- PCG, A Family of Better Random Number Generators
- Hash Without Sine
Perlin Noise
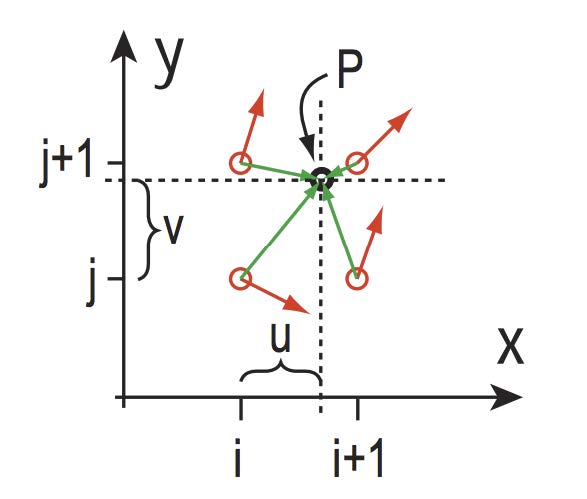
- Given a point in 2D space, find its 4 surrounding lattice points.
- Assign gradient for each lattice point with random funcion.
- Calculate distance vector for each lattice point.
- Calculate influence vector for each lattice point:
influence_vector = dot(gradient_vector, distance_vector). - Interpolate between all the influence vectors to get final value.
Worley Noise
Also known as Voronoi Noise.
- Divide the space into grids.
- Give a point in space, find its nearest N grids and generate a random position (“cell”) inside each grid.
- Calculate the minimum distance between the sample and its surrounding cells.
- Normalize the distance by dividing it with the longest possible distance.
Multi-Octave Noise
Also known as Fractional Brownian Motion (FBM)
In practice, we can combine sevral noise with different frequency together.
Octave contributions are modulated using:
- frequency: sample rate.
- persistance: decay of amplitude as frequency increases.
PerlinNoise2d(float x, float y) {
float total = 0;
float persisstence = 1 / 2.0f;
for (int i = 0; i < N_OCTAVES; ++i) {
float frequency = pow(2, i);
float amplitude = pow(persistence, i);
total += amplitude * sampleNoisei(x * frequency, y * frequency);
}
return total;
}
Implicit Surface
Approximate Normal
is the implicit surface.
Signed Distance Function
TODO
March Cubes
Divide the space into uniform grids. Sample each grid corner with the implicit surface.
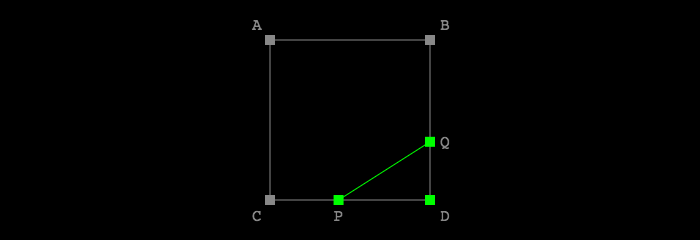
For example, ,
,
is outside,
is inside, and
,
is on the boundary (
).
